Mathematics of Diamond Pricing

A good while ago, when I was starting to look for an engagement ring, I googled, like any other reasonable human being, how to evaluate and therefore price diamonds. As you might imagine, in a decision that it’s made only once in a lifetime (hopefully), that it’s very emotionally charged, and that involve a single transaction of several thousands of dollars, being in the top results of a Google search is a very valuable thing. There is soooooo much marketing surrounding this topic, and accordingly, lots of companies will try to sell you these things. Now I want you to put your big diamond company shoes, and ask yourself this question: Would I want my consumers to be informed while selecting my diamonds?

Really ponder that question. I’ll let that on the side for a moment.

Now let me take you to another part of the world, the supplier part… Deep in a mine somewhere in #Africa, India, …. Mother earth is the real supplier here. The conditions for a diamond formation are very strict: ## add conditions That’s right, diamonds are just rocks that somebody finds in the ground. What are the chances that you are going to find 2 rocks, that can be processed into 2 diamonds with exactly D Color, VS1 Clarity, and Ideal Cut, so that one has 1 Carat, and the other 1.2 Carat to give you a perfect comparison?

This means that if you go to a jeweler, and ask for a diamond, he/she might offer you one stone like this:

Color E, Cut Ideal, Clarity VVS1, Carat 0.9

for $6387, and another:

Color D, Cut Ideal, Clarity VS1, Carat 0.9

for $5248. So which one is the good deal? The more expensive one has supposedly a better Clarity, but the cheaper one has better Color. How much of this is markup because of the neighborhood? The worst part is that these small differences in clarity, color, and cut are imperceptible to the human eye! Only experts can tell the difference using 10X lenses. I mean, just look at these pictures:

Ahhhhhrg!! So frustrating! (These diamonds have the same size, and the difference in price is $1677) They can be charging me whatever they want if I’m not able to know the right price! Eh? See what I did here? Lets go back to the question: Why would I want my consumers to be informed when selecting my diamonds? I don’t! I want them as uninformed as possible, and moreover, I want them ##deeply## emotionally invested. Perhaps if I can tie the size of the diamond to the value of the relationship…. Oh man. Marketing level > 9000.

So I was left in the shadows. But I love math. Math is like a torch of bright light diffracting through the mysteries of diamond pricing, and exposing wonderful colors of understanding.

I wrote a script and started downloading data from thousands of diamonds overnight, 19,555 diamonds to be exact. I could do some modeling with this.

Lets fix a couple of characteristics, and take a look at the price vs carat curves for different color diamonds:

Price vs Carat curve for different color diamonds of Cut Ideal and Clarity VS1. Other cuts and clarities show similar curves.

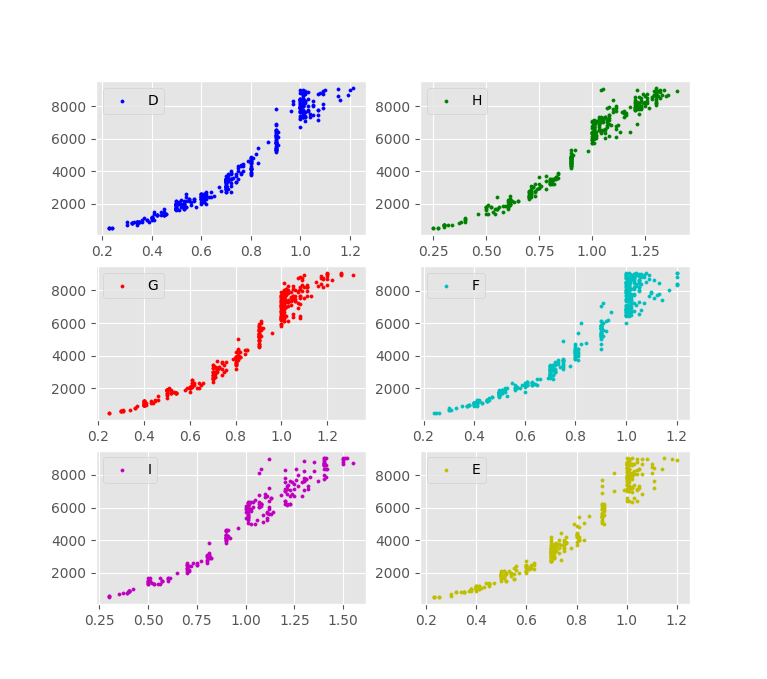Look at that nice curve. Might look like a parabola, but it can be perhaps another polynomial of higher degree, and even an exponential function

Well, let’s apply a logarithm to the carat axis and see what happens:

Wait what? it is still curvy??? It also looks exponential AGAIN??? Lets try to apply another logarithm this time to the y axis, and see what we get:

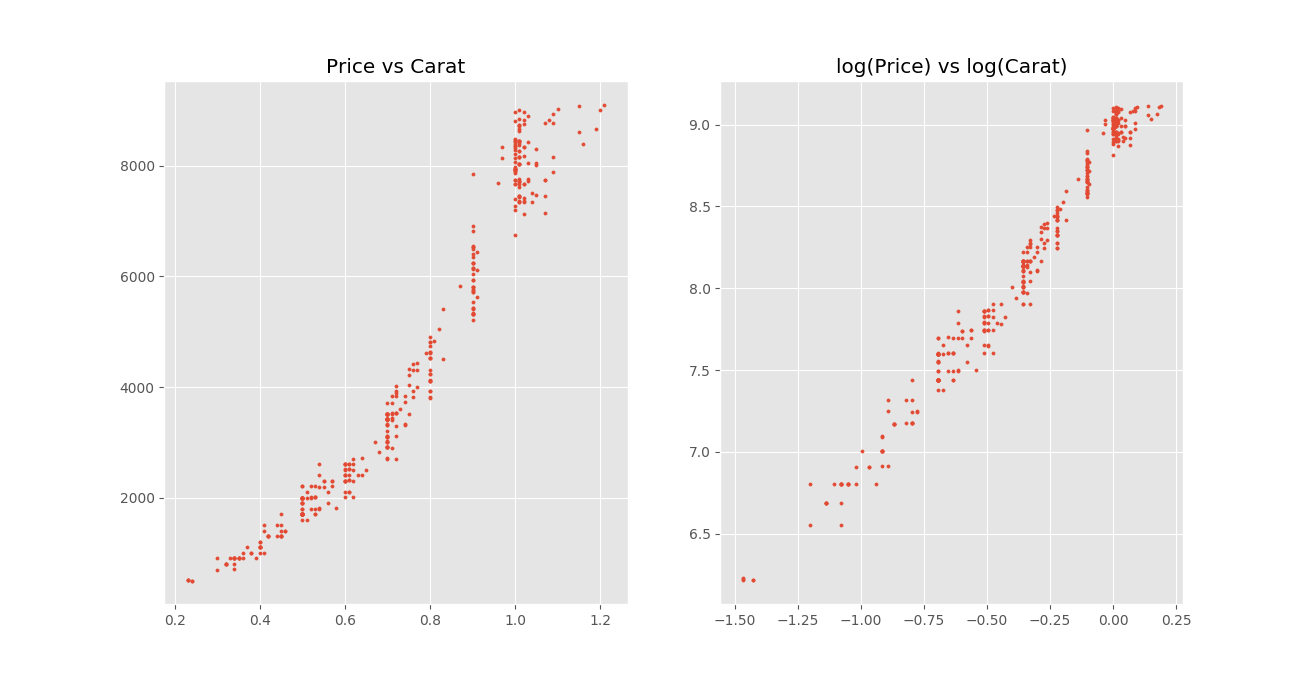Ah! Finally a decently linear scatter, which means we can do a reasonable linear interpolation on the data, i.e. obtaining parameters m, n so that we can estimate the price given a carat value (for fix Cut=’Ideal’ and Clarity=’VS1’)

\[log(y) = m log(x) + n\]

This means that the actual pricing model for diamonds is….

\[y = e^{(m log(x) + n)} = e^{(log(x^m))}e^n = x^m e^n\]

In the case of this particular data set with Cut Ideal, Color D, and Clarity VS1, we obtained from linear regression m = 2.016 and n = 8.89 (Upcoming plot of the data with the model line on it)

Now you can estimate the price of a diamond with Ideal cut and VS1 clarity if you are given the Carat of said diamond. Indeed, the estimated price from our model says: price = carat^2.016 + 8.89, so you no longer have to guess whether a given diamond has a good price or not. All you have to do is to compare the predicted price from the model derived previously with whatever the jeweler is offering; If the price offered is higher, then you know it’s not a good deal, and it’s better keep looking, but if the diamond offered is cheaper than the predicted price, then you know you have an undervalued diamond (a good deal, yay!).

This is how diamondscholar works. I constantly track the prices of thousands of diamonds, run this mathematical model for each combination of color, cut and clarity, and finally push this information so that you can make the best informed decision possible. Good luck on your search!

If you are technically inclined and want to check out the data and the model, please visit my repo on github.